在算法中,数据结构的选择直接影响程序的效率,其核心是匹配具体场景的操作需求(如频繁查找、插入、排序等)。常见数据结构可分为线性结构、树形结构、图形结构等,每种结构因存储方式和操作特性的不同,适用于特定场景。
一、线性结构:一对一的数据关系
线性结构是最基础的数据结构,元素间呈线性排列,核心差异在于内存存储方式(连续或离散)和操作效率。
| 数据结构 | 核心特点 | 优点 | 缺点 | 典型使用场景 |
|---|---|---|---|---|
| 数组(Array) | 元素连续存储,通过索引访问,长度固定(静态)或动态扩容 | 随机访问快(O(1)),内存连续利用率高 | 插入/删除效率低(需移动元素,O(n));动态扩容有性能损耗 | 需频繁随机访问场景:如存储用户列表、矩阵运算、滑动窗口算法 |
| 链表(Linked List) | 元素离散存储,通过指针/引用连接(单链表、双链表、循环链表) | 插入/删除快(O(1),只需改指针);长度灵活 | 随机访问慢(O(n),需从头遍历);额外存储指针,内存开销大 | 频繁插入/删除场景:如链表式队列、LRU缓存(双链表)、邻接表(图的存储) |
| 栈(Stack) | 遵循后进先出(LIFO),仅允许在栈顶操作(push/pop) | 操作简单,时间复杂度O(1) | 功能单一,仅支持栈顶操作 | 表达式求值(如括号匹配)、递归调用栈、深度优先搜索(DFS) |
| 队列(Queue) | 遵循先进先出(FIFO),允许在队尾插入、队头删除 | 顺序处理数据,操作效率O(1) | 中间元素操作困难 | 任务调度(如线程池任务队列)、广度优先搜索(BFS)、消息队列 |
| 双端队列(Deque) | 队列两端均可插入/删除,结合栈和队列特性 | 操作灵活,两端操作O(1) | 实现较复杂(如基于链表或循环数组) | 滑动窗口问题、缓存实现(如Java中的ArrayDeque) |
二、树形结构:一对多的层级关系
树形结构通过“父节点-子节点”形成层级,适用于具有层级关系的数据,核心是优化查找和排序效率。
| 数据结构 | 核心特点 | 优点 | 缺点 | 典型使用场景 |
|---|---|---|---|---|
| 二叉树(Binary Tree) | 每个节点最多2个子节点(左、右),无平衡要求 | 结构简单,适合递归操作 | 极端情况下退化为链表(如有序插入成单链),查找效率低(O(n)) | 基础树形结构学习,表达式树(如编译器语法解析) |
| 二叉搜索树(BST) | 左子树节点值 < 根节点值 < 右子树节点值,支持快速查找 | 查找、插入、删除平均效率O(logn) | 不平衡时退化为链表(如顺序插入) | 动态数据的查找(如字典查询),但实际中多被平衡树替代 |
| 红黑树(Red-Black Tree) | 自平衡二叉搜索树,通过颜色规则(红/黑)维持平衡,最长路径不超过最短路径2倍 | 查找、插入、删除稳定O(logn),平衡性好 | 实现复杂,旋转操作耗时 | TreeMap(Java)、C++ STL中的map/set,数据库索引(小型索引) |
| B树/B+树 | 多路平衡查找树,B树节点存储数据,B+树数据仅在叶子节点,且叶子节点连成链表 | 减少IO次数(适合磁盘存储),支持范围查询 | B+树非叶子节点不存数据,空间利用率更高 | 数据库索引(如MySQL InnoDB的聚簇索引)、文件系统(大量数据的磁盘存储) |
| 堆(Heap) | 完全二叉树,分为大顶堆(父>子)和小顶堆(父<子),支持优先操作 | 插入/删除O(logn),获取最值O(1) | 不支持随机访问,查找效率低(O(n)) | 优先队列(如任务调度按优先级执行)、堆排序、Top K问题(如取最大的10个数) |
三、哈希结构:通过哈希函数快速映射
哈希结构(Hash)的核心是键值对(Key-Value)映射,通过哈希函数将键转换为存储地址,实现快速查找。
| 数据结构 | 核心特点 | 优点 | 缺点 | 典型使用场景 |
|---|---|---|---|---|
| 哈希表(Hash Table) | 键通过哈希函数映射到数组索引,用链表/红黑树解决哈希冲突(链地址法) | 查找、插入、删除平均O(1),效率极高 | 哈希冲突处理复杂,无序,内存利用率可能低 | HashMap(Java)、缓存系统(如Redis)、用户信息存储(按ID快速查询) |
| 布隆过滤器(Bloom Filter) | 基于多个哈希函数的位图结构,判断元素“可能存在”或“一定不存在” | 空间效率极高,判断速度快 | 有误判率(不能删除元素) | 缓存穿透防护(如Redis前置过滤不存在的键)、URL去重(爬虫) |
四、图形结构:多对多的数据关系
图(Graph)由顶点(Vertex)和边(Edge)组成,用于表示复杂的关联关系(如网络连接、社交关系)。
| 数据结构 | 核心特点 | 优点 | 缺点 | 典型使用场景 |
|---|---|---|---|---|
| 邻接矩阵(Adjacency Matrix) | 二维数组存储顶点间关系(matrix[i][j] = 1表示i和j相连) | 判断两顶点是否相连快(O(1)),适合稠密图 | 空间复杂度O(n²),稀疏图浪费内存 | 稠密图(如社交网络中好友关系密集的场景),矩阵运算(如Floyd算法求最短路径) |
| 邻接表(Adjacency List) | 数组+链表,数组存顶点,链表存相邻顶点 | 空间效率高(O(n+e),e为边数),适合稀疏图 | 判断两顶点是否相连慢(O(k),k为邻接顶点数) | 稀疏图(如互联网拓扑结构)、图的遍历(DFS/BFS),路由算法(如最短路径计算) |
五、其他常用结构
| 数据结构 | 核心特点 | 典型使用场景 |
|---|---|---|
| 字符串(String) | 字符序列,支持拼接、截取、匹配等操作,通常以数组存储(如C语言)或对象封装(如Java String) | 文本处理(如搜索引擎分词)、正则表达式匹配、DNA序列分析 |
| 并查集(Union-Find) | 管理元素分组,支持“合并集合”和“查询元素所属集合”操作,通过路径压缩和按秩合并优化 | 连通性问题(如判断网络中两台设备是否连通)、最小生成树(Kruskal算法) |
| 字典树(Trie) | 前缀树,字符作为节点,路径表示字符串,适合前缀匹配 | autocomplete(自动补全)、拼写检查、IP路由最长前缀匹配 |
六、选择数据结构的核心原则
- 操作频率优先:若频繁查找,优先哈希表、红黑树;若频繁插入删除(中间位置),优先链表;若需维持顺序且快速取最值,优先堆。
- 数据规模适配:小规模数据用数组即可(简单);大规模数据需考虑内存效率(如B+树适合磁盘存储)。
- 平衡时间与空间:哈希表用空间换时间(O(1)查找但需处理冲突);链表用时间换空间(内存灵活但访问慢)。
总结:数据结构的本质是“操作效率的适配”
没有万能的数据结构,只有最适合场景的选择。理解每种结构的核心操作效率(查找、插入、删除的时间复杂度)和内存特性,才能在算法设计中做出最优决策。例如,同样是查找,哈希表适合单值查询,而B+树适合范围查询;同样是排序,堆排序适合动态数据(边插入边排序),而快速排序适合静态数据一次性排序。掌握这些特性,是解决算法问题的基础。
排序算法
排序算法是计算机科学中用于将一组数据按照特定顺序(如升序、降序)排列的方法,常见的排序算法可以根据原理和特性分为以下几类,每类包含多种具体实现:
一、比较类排序(通过比较元素大小确定顺序)
基于元素之间的比较进行排序,时间复杂度下限为 O(n log n)(基于决策树模型)。
1. 交换排序(通过交换元素位置实现)
-
冒泡排序(Bubble Sort)
- 原理:重复遍历数组,每次比较相邻元素,若顺序错误则交换,直到无需交换(即数组有序)。
- 特点:简单直观,稳定(相等元素相对位置不变),时间复杂度 O(n²)(最坏/平均),空间复杂度 O(1),适合小规模数据。
-
快速排序(Quick Sort)
- 原理:选择一个“基准值”,将数组分为两部分(小于基准和大于基准),再递归排序两部分。
- 特点:分治法思想,不稳定,平均时间复杂度 O(n log n),最坏 O(n²)(如已排序数组选两端为基准),空间复杂度 O(log n)(递归栈),实际应用中最常用。
2. 插入排序(通过插入元素到合适位置实现)
-
直接插入排序(Insertion Sort)
- 原理:将数组分为“已排序”和“未排序”部分,每次从后者取一个元素插入前者的正确位置。
- 特点:稳定,时间复杂度 O(n²)(最坏/平均),O(n)(最好,已排序数组),空间复杂度 O(1),适合小规模或基本有序数据。
-
希尔排序(Shell Sort)
- 原理:先将数组按一定“步长”分组,对每组进行插入排序,逐步减小步长至1(最后一次为直接插入排序)。
- 特点:不稳定,时间复杂度取决于步长(如最优步长下约 O(n^1.3)),空间复杂度 O(1),效率高于直接插入排序。
3. 选择排序(通过选择最小/大元素放置到位实现)
-
直接选择排序(Selection Sort)
- 原理:每次从“未排序”部分选最小(大)元素,与未排序部分的首位交换,直至排序完成。
- 特点:不稳定(如交换时破坏相等元素顺序),时间复杂度 O(n²)(无论数据状态),空间复杂度 O(1),适合简单场景。
-
堆排序(Heap Sort)
- 原理:利用堆(完全二叉树)的特性,先构建大顶堆(或小顶堆),反复将堆顶元素(最大/小)与末尾元素交换并调整堆,直至排序完成。
- 特点:不稳定,时间复杂度 O(n log n)(最坏/平均),空间复杂度 O(1),适合大规模数据。
4. 归并排序(通过合并有序子数组实现)
- 归并排序(Merge Sort)
- 原理:分治法思想,将数组递归拆分为两半,分别排序后合并两个有序子数组。
- 特点:稳定,时间复杂度 O(n log n)(最坏/平均),空间复杂度 O(n)(需要额外空间存储合并结果),适合大规模数据,尤其外部排序(数据不能全部加载到内存时)。
二、非比较类排序(不通过比较元素大小,依赖元素本身特性)
时间复杂度可突破 O(n log n),但对数据有特殊要求(如整数、范围有限等)。
-
计数排序(Counting Sort)
- 原理:假设元素值在 [0, k] 范围内,统计每个值的出现次数,再根据次数计算元素的位置。
- 特点:稳定,时间复杂度 O(n + k)(n 为元素数,k 为值范围),空间复杂度 O(n + k),适合值范围小且为整数的数据(如成绩排序)。
-
桶排序(Bucket Sort)
- 原理:将元素分到多个“桶”中,每个桶内部用其他排序算法(如插入排序)排序,最后合并所有桶。
- 特点:稳定(取决于桶内排序算法),时间复杂度 O(n + k)(理想情况下,元素均匀分布),空间复杂度 O(n + k),适合元素分布均匀的数据。
-
基数排序(Radix Sort)
- 原理:按元素的“基数”(如个位、十位)依次排序,先排低位再排高位,依赖计数排序或桶排序作为子过程。
- 特点:稳定,时间复杂度 O(d(n + k))*(d 为基数位数,k 为基数范围),空间复杂度 O(n + k),适合整数或可转化为固定位数的字符串(如手机号)。
各类排序算法对比表
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 最好时间复杂度 | 空间复杂度 | 稳定性 | 适用场景 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n²) | O(n²) | O(n) | O(1) | 稳定 | 小规模、基本有序数据 |
| 快速排序 | O(n log n) | O(n²) | O(n log n) | O(log n) | 不稳定 | 大规模数据(实际应用最广) |
| 直接插入排序 | O(n²) | O(n²) | O(n) | O(1) | 稳定 | 小规模、基本有序数据 |
| 希尔排序 | O(n^1.3) | O(n²) | O(n) | O(1) | 不稳定 | 中等规模数据 |
| 直接选择排序 | O(n²) | O(n²) | O(n²) | O(1) | 不稳定 | 简单场景,对稳定性无要求 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | 不稳定 | 大规模数据,对空间敏感 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 稳定 | 大规模数据,需稳定性 |
| 计数排序 | O(n + k) | O(n + k) | O(n + k) | O(n + k) | 稳定 | 整数,值范围小 |
| 桶排序 | O(n + k) | O(n²) | O(n + k) | O(n + k) | 稳定 | 元素分布均匀的数据 |
| 基数排序 | O(d*(n + k)) | O(d*(n + k)) | O(d*(n + k)) | O(n + k) | 稳定 | 整数或固定位数字符串 |
选择排序算法时,需根据数据规模、是否需要稳定排序、数据分布特性(如是否有序、值范围)等因素综合考虑。例如,小规模数据可选插入排序,大规模数据常用快速排序或归并排序,对空间敏感选堆排序,整数且范围小选计数排序等。
归并和快速排序区别
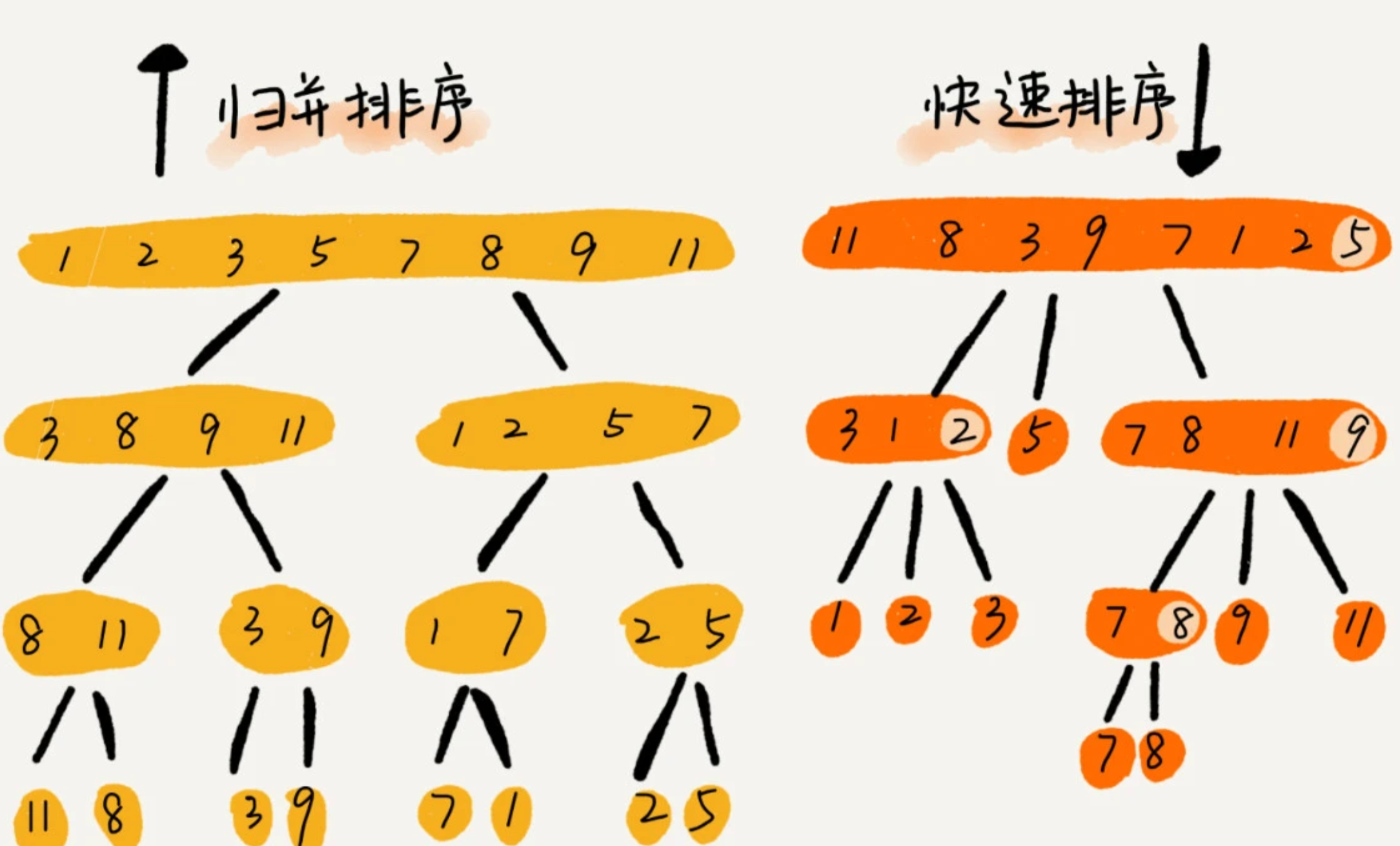
三、Go 排序
在 Go 语言中,排序功能主要通过标准库 sort 包实现,该包提供了通用的排序接口和多种排序算法的实现。下面介绍 Go 中排序的核心原理、标准库实现以及常见排序算法的手动实现。
一、Go 排序的核心接口:sort.Interface
Go 的排序设计采用接口抽象,任何类型只要实现了 sort.Interface 接口,就能使用 sort 包的排序函数。该接口定义了三个方法:
type Interface interface {
Len() int // 返回元素数量
Less(i, j int) bool // 比较索引 i 和 j 的元素(i < j 时返回 true)
Swap(i, j int) // 交换索引 i 和 j 的元素
}
- 原理:通过这三个方法,
sort包可以独立于具体数据类型(切片、结构体等)进行排序,实现了“算法与数据分离”。
二、标准库 sort 包的底层算法
Go 的 sort 包并非固定使用某一种算法,而是根据数据类型和长度自适应选择最优算法,以平衡性能:
-
插入排序(Insertion Sort):
- 适用场景:数据量小(
n ≤ 12)或接近有序的切片。 - 原理:将元素逐个插入到已排序部分的正确位置,时间复杂度
O(n²),但小数据场景下常数项低,效率高。
- 适用场景:数据量小(
-
快速排序(Quick Sort):
- 适用场景:中等大小的切片(
12 < n ≤ 1000)。 - 原理:选基准值分区,递归排序左右子数组,平均时间复杂度
O(n log n)。Go 采用“三数取中”(首、中、尾元素的中间值)选基准,避免极端情况。
- 适用场景:中等大小的切片(
-
归并排序(Merge Sort):
- 适用场景:大数据量(
n > 1000)。 - 原理:分治思想,将数组分成两半分别排序,再合并,时间复杂度稳定
O(n log n),但需额外空间。
- 适用场景:大数据量(
三、常见排序算法的 Go 实现
1. 快速排序(Quick Sort)
原理:选基准值,分区(小于基准放左,大于放右),递归排序子数组。
package main
import "fmt"
// 快速排序:对整数切片排序
func quickSort(nums []int, left, right int) {
if left >= right {
return
}
// 分区,返回基准值位置
pivot := partition(nums, left, right)
// 递归排序左右子数组
quickSort(nums, left, pivot-1)
quickSort(nums, pivot+1, right)
}
// 分区函数:选最右元素为基准
func partition(nums []int, left, right int) int {
pivotVal := nums[right] // 基准值
i := left - 1 // 小于基准的区域边界
for j := left; j < right; j++ {
if nums[j] <= pivotVal {
i++
// 交换到小于基准的区域
nums[i], nums[j] = nums[j], nums[i]
}
}
// 基准值归位(放到小于区域的右边)
nums[i+1], nums[right] = nums[right], nums[i+1]
return i + 1
}
func main() {
nums := []int{3, 1, 4, 1, 5, 9, 2, 6}
quickSort(nums, 0, len(nums)-1)
fmt.Println(nums) // 输出:[1 1 2 3 4 5 6 9]
}
2. 归并排序(Merge Sort)
原理:分治思想,将数组二分至最小单元,排序后合并。
package main
import "fmt"
// 归并排序:对整数切片排序
func mergeSort(nums []int) []int {
if len(nums) <= 1 {
return nums
}
// 二分
mid := len(nums) / 2
left := mergeSort(nums[:mid])
right := mergeSort(nums[mid:])
// 合并
return merge(left, right)
}
// 合并两个有序切片
func merge(left, right []int) []int {
res := make([]int, 0, len(left)+len(right))
i, j := 0, 0
// 比较并合并
for i < len(left) && j < len(right) {
if left[i] < right[j] {
res = append(res, left[i])
i++
} else {
res = append(res, right[j])
j++
}
}
// 追加剩余元素
res = append(res, left[i:]...)
res = append(res, right[j:]...)
return res
}
func main() {
nums := []int{3, 1, 4, 1, 5, 9, 2, 6}
fmt.Println(mergeSort(nums)) // 输出:[1 1 2 3 4 5 6 9]
}
3. 插入排序(Insertion Sort)
原理:从第二个元素开始,逐个将元素插入到前面已排序部分的正确位置。
package main
import "fmt"
// 插入排序:对整数切片排序
func insertionSort(nums []int) {
for i := 1; i < len(nums); i++ {
key := nums[i] // 待插入元素
j := i - 1
// 移动前面大于 key 的元素
for j >= 0 && nums[j] > key {
nums[j+1] = nums[j]
j--
}
// 插入 key
nums[j+1] = key
}
}
func main() {
nums := []int{3, 1, 4, 1, 5, 9, 2, 6}
insertionSort(nums)
fmt.Println(nums) // 输出:[1 1 2 3 4 5 6 9]
}
四、使用标准库 sort 包排序
对于常见类型(如 []int、[]string),sort 包提供了简化函数(如 sort.Ints、sort.Strings),无需手动实现接口:
package main
import (
"fmt"
"sort"
)
func main() {
// 排序整数切片
nums := []int{3, 1, 4, 1, 5}
sort.Ints(nums)
fmt.Println(nums) // [1 1 3 4 5]
// 排序字符串切片(按字典序)
strs := []string{"banana", "apple", "cherry"}
sort.Strings(strs)
fmt.Println(strs) // [apple banana cherry]
// 自定义结构体排序(需实现 sort.Interface)
type Person struct {
Name string
Age int
}
people := []Person{
{"Bob", 31},
{"John", 42},
{"Alice", 23},
}
// 按年龄排序
sort.Slice(people, func(i, j int) bool {
return people[i].Age < people[j].Age
})
fmt.Println(people) // [{Alice 23} {Bob 31} {John 42}]
}
五、总结
- Go 排序设计:通过
sort.Interface接口实现通用排序,算法自适应选择(小数据插入排序、中数据快速排序、大数据归并排序)。 - 手动实现:快速排序适合中等数据,归并排序适合大数据(稳定),插入排序适合小数据或接近有序场景。
- 最佳实践:优先使用标准库
sort包(如sort.Ints、sort.Slice),其经过优化,性能优于手动实现的简单版本。
Go 的排序实现兼顾了灵活性和性能,是处理各种排序场景的高效工具。